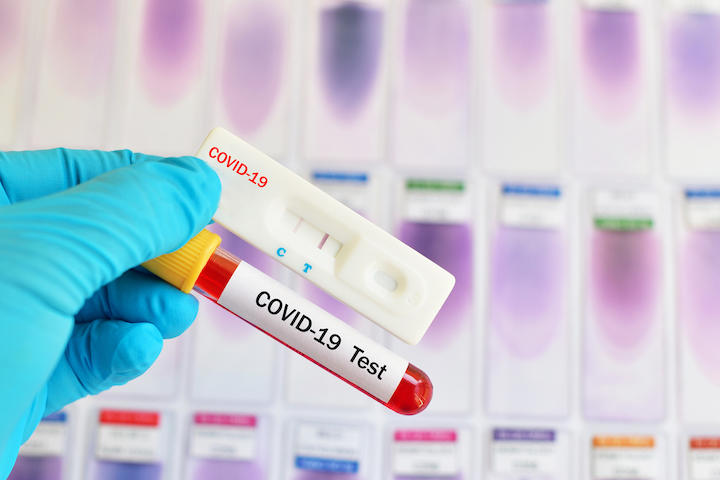
８割減にするには、外出を半分にすればよい

なんとなく 精神的にかったるいですね。新型コロナウイルスのために外出を控えているためです。

運動不足です。部屋の中でスクワットや、先のブログで紹介したような体操はやっておりますが、それでもまだまだ足りません。

緊急事態宣言のさなかに、検察庁法改正案をゴリ押ししようとか、「それ、今やることか？」と、それもストレスの一因です。

緊急事態宣言が解除されそうな報道ですが、東京都内はまだ無理でしょう。でも感染者数も陽性率も下がってはきています。

実際の感染者数は10倍とか20倍、いや30倍だと言う尾身茂さんの国会での答弁もありましたけども、下降曲線に入っていることは確かだと思われます。

でもこれは国民が必死の思いで耐えて自粛をした結果です。

8割おじさんが言うように、人との接触を8割減らす。しかし、実際は8割以上減らしたのではないでしょうか。

どういうことかと言うと、ニュースでは、渋谷の交差点の人の流れが、コロナの拡散する前に比べてこれだけ減りました。あるいは湘南の海岸では以前に比べて何パーセント減りましたと言ってますけども、減り方が少ないというニュアンスでの伝え方が多かったですね。

「半分程度にしか減っていません」というような報道でした。

でも8割おじさんが言ってるのは、人と人との接触を8割方減らすということであって、人の流れを8割減らすということではなかったはずです。

部屋に２人の人間しかいなければ接触する機会は1です。ところが部屋に10人がいると接触する機会は45になります。人の数が5倍になると接触する機会は45倍になるのです。

これは統計でいう順列・組み合わせの、組み合わせの問題です。 n人から2人を選ぶ場合の組み合わせは何通りあるかということですね。

n（人の流れ）が十分に大きければ、

$$ 人との接触=\displaystyle {}_n C_2 = \frac{n!}{2! (n-2)!} \approx \frac{n^2}{2} $$

となります。

ｎが十分に大きければ、組み合わせの数は \( n^2 \)に比例します。

人と人の接触を \( \frac{1}{5} \) にするには、人の流れ n を、

$$ 人の流れ(ｎ)=\frac{1}{\sqrt{5}}  \approx 0.447 $$

とすればよいのです。

つまり、人の流れをこれまでの半分強減らして45％程度にすれば、人との接触の機会は80％減ります。

８割おじさんの目的はこれで達成できるわけです。

リモートワークのできない職種もありますから実際には何割減ったのかはわかりませんが、私の感覚では、ここまで減らさなくてもウイルス感染の機会や罹患者は減ったのではなかろうかと思っています。

ホテルや飲食店、航空会社にJR など、さまざま業種に経済的な影響が出ていますが、第2波が来て、もう一度緊急事態だと言われても、そりゃできないよ、死んでしまうよ、という人が増えるのではないでしょうか。

東京都の陽性率もやっと出るようにはなって、5%程度に下がってきました。

あのグラフを見ても、いまいち不信感が拭えません。死者の数が急に増えちゃったりしてますからね。きちっとデータ管理をし、科学的根拠に基づいて規制をして欲しいものです。