エビデンスだけでがん治療ができるのか？（４）

マーク・トウェインは「世の中には3種類の嘘がある: 嘘、大嘘、そして統計だ」と言ったそうです。統計の持つ特徴を的確に表しています。『統計で嘘をつく方法』という本もありましたね。

「10人の患者が〇〇療法をやったら、１人のがんが消えました」これは真実を言っているのでしょう。しかし、「あなたのがんの1/10は消えます」は、だれでもウソだと分かります。「あなた」にとってはゼロ％か100％かのどちらかです。エビデンスのある治療法を受けたからといって、エビデンス通りの治療効果があるとは誰も保証できません。

統計的な有意差が証明されているからから、この治療法は正しいと考えるのも短絡的で、統計の嘘に翻弄されているのでしょう。

Aという薬剤に対して、95％の確率で治療した人と治療していない人のアウトカム（生存率など）に「差がある」と考えて良いだろうとの結果がでた場合、「95％以上の確率で有意　＝　P＜0.05で有意」という言い方をします。

すると、めでたくエビデンスがある、ガイドラインに載ることになるわけです。

しかし、これは20回に1回は有意差がない＝効果は違わないということです。医学の世界では「20回に1回ウソをつくことはご容赦を」というルールがあるのです。

尾藤誠司氏(東京医療センター臨床研修科医長)が、「P値⇒ピーチ⇒桃」のだじゃれで、『バルサルタン問題に思う～桃の誘惑にご用心』を日経メディカルに書いています。

ある数字がP<0.05 なら治療は有効と認識され、P>0.05なら治療は無効と認識されることが一般的なのです。
しかし、以上の様な認識はいろいろな意味で間違っています。

間違いの一つは、「有効でないなら無効」という考え方です。
統計学的にいくら「有効」な治療であったとしても、その有効性がわずかなものであれば、それは臨床においては「使えない」治療です。
よく、大規模臨床試験で有効性が確認されたからすごい、というような解釈がありますが、逆に捉えれば、大規模なサンプル数がなければ有効性が確認されないような治療というのは、恐らく劇的な効果が期待できないということも言えるのです。一方で、統計学的には有意でなかったとしても、結果の傾向を見ればこの患者さんには適応できるのではないか、というような解釈は可能なはずです。

もう一つの間違いは、そもそも95%の確からしさ、すなわちP<0.05を持って意味があるとすること自体に特に根拠がない、ということです。「P<0.05をもって有意とする」という認識は、暫定的に運用している理不尽なルールに過ぎないのです。しかしながら、臨床研究の世界はまさにこの「P値」を求め続けることで回ってしまっています。

研究のデザインや、データの定義、データを集めるプロセス、そしてデータ解析のプロセスなど、臨床研究における様々なプロセスにおいて結果の統計学的有意差は左右されていきます。そして、P<0.05となるような有意な差を結果にもたらそうとする誘惑に研究者はいつもかられているのです。これを私は「桃(ピーチ)の誘惑」と呼んでいます。

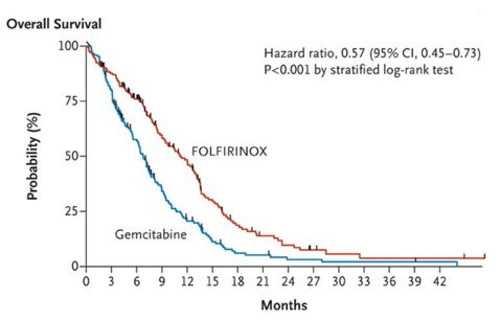
統計学的に「有効」であっても、その差がわずかなら臨床においては「使えない」治療です。膵臓がんにおけるタルセバがよい例です。ごくわずかの違いしかないのに、間質性肺炎などの危険性があるので、いまではほとんどの医療機関で使われていません。

「統計とは、ごくわずかの違いしかないときに、相手を説得する技術である」

逆に、統計的有意差がない(P>0.05)ことは、効果がないことにはなりません。P値だけに関心が向いていると、いわゆるβエラー(第二種の過誤:本当は差があるのに、ないとする誤り。ぼんやりエラーともいう)に陥ることもあります。

P値だけに囚われるなとNEJMも統計学会も警告

P値と統計的有意差があるなしだけを判断の基準とすることに対して、世界的権威のある医学誌が論文で注意を促しているのです。1978年New England Journal of Medicine (NEJM)に特別論文が掲載され、統計的な有意差がないために「Negative」とされた71編の臨床試験の結果のうち、点推定値と区間推定値で示すと、実は「Positive」な影響があったと思えるものが多数あることが分かったとし、βエラーを考慮することの重要性を強調しています。

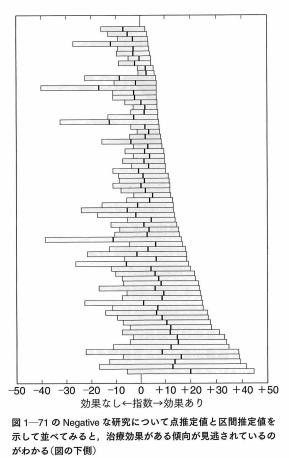
このグラフの下側の試験結果を見れば、明らかに治療効果があることが見て取れます。統計的に有意差がないことと効果がないことを混同してはならないこと、それを防ぐために点推定値と区間推定値の重要さが指摘されているのです。

また、こうした“P値信仰”ともいうべき風潮に関して、米国統計学会は2016年3月に声明を発表しました。「Statisticians issue warning over misuse of P values」（Nature. 2016;531:151.）この中で、「科学的な結論、ならびにビジネスや政策上の判断は、P値が特定の閾値を超えるかどうかだけに基づいてなされてはならない」とはっきりと述べられています。

しかし日本の医師は、いまだにP値だけをありがたがり、90％信頼区間などの区間推定値に関心がありません。

100人のうち51人に効果があれば標準治療、49人ではダメ

”あんたの話は難しい”という方のために、上の説明を比喩で言い換えますと、標準治療は100人のうち51人に効果がなければならず、49人ではダメなんです。国民の納めた保険料を使うのだから当然です。しかし、ダメな治療法の中には49人に効果のある治療法もあれば、1人あるいは0人にしか効果がない治療法も、10人に効果のある治療法もあるはずです（区間推定値の重要性）。がん患者から見れば、統計的に有意差がない ＝エビデンス（科学的な根拠）がなくても、100人で10人に効果がある治療法なら、希望が持てるのです。