がんと自己組織化臨界現象 (2)

砂山ゲーム

1987年、ニューヨークにあるブルックヘブン国立研究所の一室で、3人の理論物理学者が奇妙なゲームを始めました。テーブルの上に砂粒を一粒ずつ落としていったら何が起きるのかという問題に挑戦していたのです。何が起きるかは明白です。砂山は段端と高くなっていき、ある時点で一粒の砂が引き金となって雪崩が起きるでしょう。その結果山は低くなり、さらに砂粒を落としていけば、高くなる。ある時点で雪崩が発生して山は低くなり・・・と山の輪郭は永遠に変化を繰り返します。

実際には、彼らはテーブルの上ではなくパソコン上に仮想のテーブルを設定
して、その上に砂粒を落としていったのです。彼らの疑問は、雪崩には典型的な大きさはあるのか？　次に起きる雪崩の大きさを予想することはできるか？というものでした。

防衛大学校の岩瀬康行さんがこの砂山モデルをJavaアプレットで動作するようにプログラム化されています。「自己組織化臨界現象(SOC)のページ」

「砂山モデルアプレット」をクリックすれば50×50のマス目（仮想テーブル）が表示されるので、「Start」ボタンをクリックして砂を落としはじめます。1～2時間程度はアプレットを走らせる必要があります。しばらく放っておきましょう。

さて、3人の物理学者の実験に話を戻します。彼らは雪崩の大きさ(砂粒の数)と頻度の関係を数えたのです。その結果「典型的な」雪崩というものは存在しないことを発見したのです。あるときは1粒だけ、あるときは100粒、ときには1000粒が崩れ落ちたのですが、次にどんな規模の雪崩になるかは「予測不可能」でした。

砂粒を落としていけば自然と砂山ができるという意味で、砂山は「自己組織化」されている。雪崩が起きるまでは、この自己組織化された砂山は「安定状態」にある。しかし、黄色の領域がまだら状にに増えてくれば不安定になり、次の1粒が何を引き起こすかは予測不可能になります。この状態が「臨界状態」です。

「臨界状態」は多くの物理現象で見られます。1気圧下での水は100℃で液体から気体になります(相転移）。このとき水は臨界点にあると言います。鉄は770℃で強磁性体から常磁性体に相転移します。この温度がキュリー温度です。

しかし、これらの臨界状態は特殊な条件（水は100℃、鉄は770℃）でしか見ることはできません。温度がほんの少し変わっても臨界状態は維持できないのです。このように臨界状態は不安定で希な現象であると見なされてきました。ところが砂山モデルでは、何も考えずに砂粒を落としていくだけで、このような状態が自ずから必然的に現われてくるのです。

不安定な臨界状態が組織化される現象は、世界中に普遍的に存在しているようなのです。あらゆる物事のネットワークは、どれもみな同じ方法で自らを組織化していくことが、多くの物理学者の引き続いた研究によって明らかになってきました。

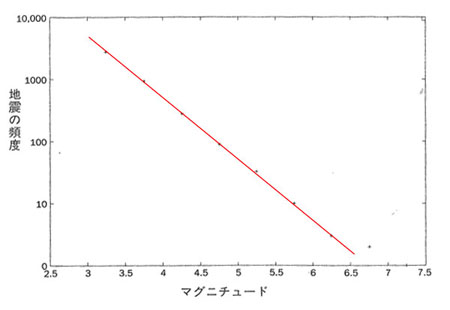
そしてこの砂山ゲームにおいてもべき乗則が現われてきました。横軸に雪崩の大きさの対数、縦軸に全体に対する割合の対数をとると、みごとな直線関係が表われてくるのです。先のアプレットを2時間走らせた結果が右の図です。

べき乗則が成り立つ自己組織化臨界現象においては、「歴史」が重要な意味を持つのです。ひとつの砂粒がある位置に置かれたとき、その砂粒は以後の現象に永遠に影響を与えることになります。ニュートンの万有引力の法則は、今日も100年前も1000年後も同じであり、時間（歴史）によって変わることはありません。しかし、このべき乗則が成立するシステムにおいては、「今ここで起きたことが、未来全体にずっと影響を与え続ける」のです。平衡状態からはずれた系においては、時間の経過（歴史）が重要な意味を持つわけです。

たったひとつの細胞から発達してきた生物に関しては、これはあたりまえすぎることかもしれません。今あなたの体内にあるひとつのがん細胞が、未来全体に影響を与えるのです。

森林火災モデル

森林火災でも同じべき乗則が見つかっています。簡単に触れることにします。

アメリカ合衆国とオーストラリアで過去一世紀の間に起きた森林火災の焼失面積と発生件数をグラフにすると、やはりべき乗則が現われてきました。コーネル大学の研究者らは、砂山モデルと同じようにコンピュータでシミュレーションを行ないました。先の砂山モデルで、マス目は樹木の密度に応じて色分けされていると考え、そこにマッチを落とすと赤く変わると考えれば、雪崩の大きさを森林火災の大きさと見なすことができます。結果は同じべき乗則になるのです。

スケールに依存しないというべき乗則の性質は、大規模なできごとは単に小規模なできごとを拡大しただけのものであり、それらは同じ原因で発生するということを示しています。大地震にも大規模森林火災にも特別な原因があるわけではないのです。

このほかにも、バッタの大発生、はしかの流行、交通渋滞の発生、株式の暴落＝恐慌の発生、中性子星パルサーの自転周期などにもべき乗則が見つかっています。

「手の甲に水を一滴落とすとしましょう。その水滴は、手の甲を滑り落ちていく。滑り落ちる先は手首かもしれない。親指かもしれない。指のあいだかもしれない。どこに落ちるかはわかりません。しかし、この手の表面のどこかを伝わって落ちることだけは確かだ。」

****

「マルカムのモデルには、突起や急勾配の斜面–つまりその水滴の移動速度がぐんと大きくなる場所がたびたび現われます。その速度が速くなる現象を控えめに表現したのが、マルカム効果というわけです。つまり、システム全体はいつ急激に崩壊するかもわからない。そして、＜恐竜王国＞についてもそれはあてはまる。そう、マルカムはいうんですよ。＜王国＞には本質的な不安定さがあるとね。」

『ジュラシック・パーク〈下〉 (ハヤカワ文庫NV)
』より。

　　　　　　　　　　　　　　　　　　　　　　　　　（つづく）